Teorema de Bayes y calabacines
Un poco más de estadística para iniciados: el teorema de Bayes es uno de los más chachis de la teoría de la probabilidad, ya que permite calcular la probabilidad a posteriori. Una de esas cosas que cuando nos la explicaron en la uni en mi caso simplemente se quedó en una fórmula, sin saber muy bien cuándo se aplicaba. Una vez más, la iluminadora asignatura de minería de datos de mi máster, me ha hecho entender cosas que debería dominar desde hace años.
Además de las aplicaciones que tiene este teorema en la minería de datos, con los clasificadores bayesianos, este teorema tiene aplicación cotidiana, que ilustraré con un ejemplo calabacinil:
Tenemos la explotación agrícola del tío Bayu, que produce 8000 calabacines por lote, de los cuales un 5% son calabacines amarillos, de exquisitas propiedades.
Por otro lado, la malévola granja del Dr. Pimiento produce 12000 calabacines por lote (es una gran explotación), pero un 2% de los calabacines son amarillos, y sabemos que los calabacines amarillos del Dr Pimiento son muy malignos y en cualquier momento pueden atacarnos mientras dormimos.

Las dos granjas venden a un mercado, y yo que compro en él me encuentro con que uno de los calabacines que me han vendido es amarillo. Pero ¡¿cómo sé de qué granja es!? ¿Me juego la vida y lo mantengo en la nevera o mejor lo destruyo? Bayes me puede ayudar!
Porque lo que necesito saber es la probabilidad de que el calabacín amarillo sea de la granja del tío Bayu, es decir, una probabilidad a posteriori.
Vale, pues Bayes me dice que

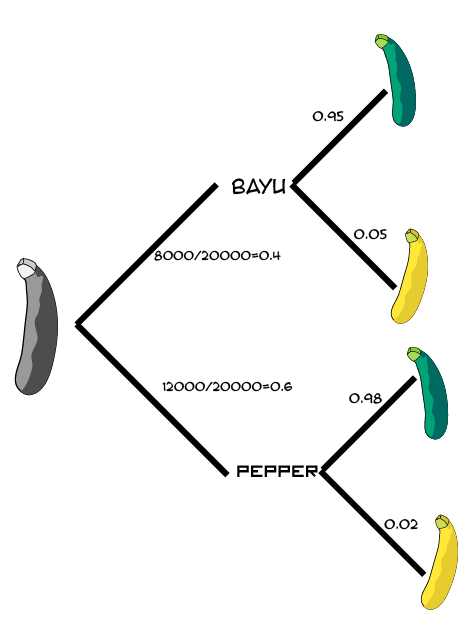
La P(Ai|B) es la probabilidad de que el suceso Ai se dé cuando se da B, en este caso, B es ser amarillo (lo conocemos), y Ai es ser de la Granja del tío Bayu. En el numerador se multiplica la probabilidad inversa, que conocemos, es decir, que siendo de la Granja del Tío Bayu, sea Amarillo (0.05) por la probabilidad de que sea de la granja del tío Bayu P (Ai). Que si hay 20000 calabacines en total, y 8000 son de esta granja, la probabilidad será de 0.4
En el denominador se suman todos los otros casos en los que hay calabacines amarillos.
Es decir, traduciendo el teorema anterior a nuestro caso:
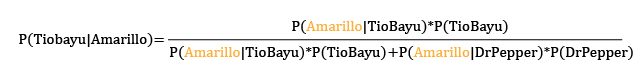
Y ahora, si traducimos esas probabilidades con el árbol anterior:
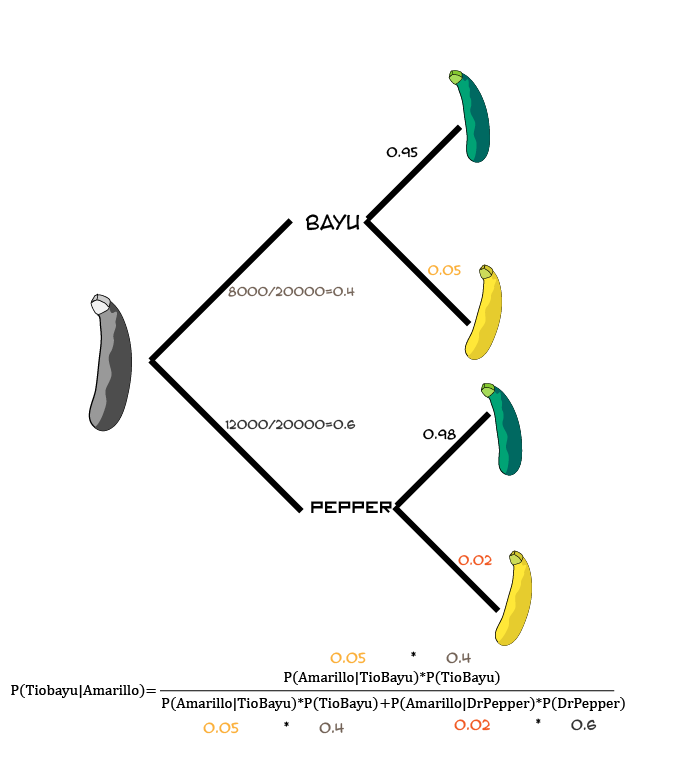 Por lo que…
Por lo que…

con lo cual, la probabilidad de que sea de la granja del tío Bayu es del 62,5%, así que parece poco seguro quedárselo en la nevera. Bah, nos la jugamos!
Oh no! Olvidaba que había aún un 37,5% de probabilidades de que fuera uno de los calabacines amarillos del Dr. Pimiento
NOOOOO

7 comentarios sobre “Teorema de Bayes y calabacines”
Salvas de aplausos. Ovación cerrada. La divulgación científica con calabacines es insuperable.
Totalmente de acuerdo con Mos. Me encantan estos post calabaestadísticos!
Lol, alguien los lee!!!
próxima entrega: regresión lineal!
(edit): alguien los lee, aunque sea necesario publicarlo en face.. :P
edit 2: y veo que no lo habéis leído muy a fondo pq he descubierto un par de erratas, ya subsanadas! :D
Está claro que llego a la versión corregida ;-)
Interesante sí, la calabacinología aplicada!
:D